- Mechanics
- /
- Static
- /
- Static of a particle
Static is a branch of mechanics that studies the forces acting on objects that are at rest. The static is particularly important in the construction of buildings, bridges, viaducts and other structures that should be at rest (static).
Static Particle
It is important to differentiate a rigid body from a particle.
- Particle
- Particle or material point is any object whose dimensions are very small when compared with the other dimensions involved in the problem. When we consider an object as a particle, we are assuming that the rotational effects are not important in the study. For example, the Earth can be considered a particle if we are studying only its movement around the sun.
- Rigid Body
- It is one that hardly suffers deformation when under the action of the forces acting on it. The dimensions affect the analysis of the equilibrium; that is, it can not be treated as a particle. For example, a seesaw board cannot be considered a particle, because the application of the force (normal) position that children make in the seesaw will influence its balance.
- Center of Mass
- In cases where it is possible to treat an extensive body as a punctual particle, it is considered that the whole mass of the body is located at a point. This is known as center of mass or center of gravity. In the case of a homogeneous object, this point is the centroid or geometric center of the body. This is where we draw the weight vector.
Conditions of Static Equilibrium of a Particle
From Newton's First Law, it is known that: for a particle at rest to remain in this state, it is necessary that the net force on it is zero. Mathematically we have: $$\vec{F}_{net} = \sum_i^n \vec{F}_i = \vec{0},$$ where \(\vec{F}_{net}\) is the resultant force and \(\vec{F}_i\) are the \(n\) forces acting on the system. We can rewrite this explicitly in terms of the horizontal components \(x\) and vertical \(y\) , thus obtained: \begin{array} \\ F_{net,x} = \sum_i^n \pm F_{i,x} =\\ = \pm F_{1,x} \pm F_{2,x} \pm ... \pm F_{n,x} = 0,\\ F_{net,y} = \sum_i^n \pm F_{i,y} =\\ = \pm F_{1,y} \pm F_{2,y} \pm ... \pm F_{n,y} = 0, \end{array} where \(F_{net,x}\) and \(F_{net,y}\) are the algebraic values of the horizontal and vertical components of the net force, that is, the magnitude of the force and the algebraic sign indicating the direction of it. Respectively, \(F_{i,x}\) and \(F_{i,y}\) are the magnitudes of the components of the forces acting on the system, and the signal \((\pm)\) in front of the module must be chosen appropriately, according to the direction of the force component.
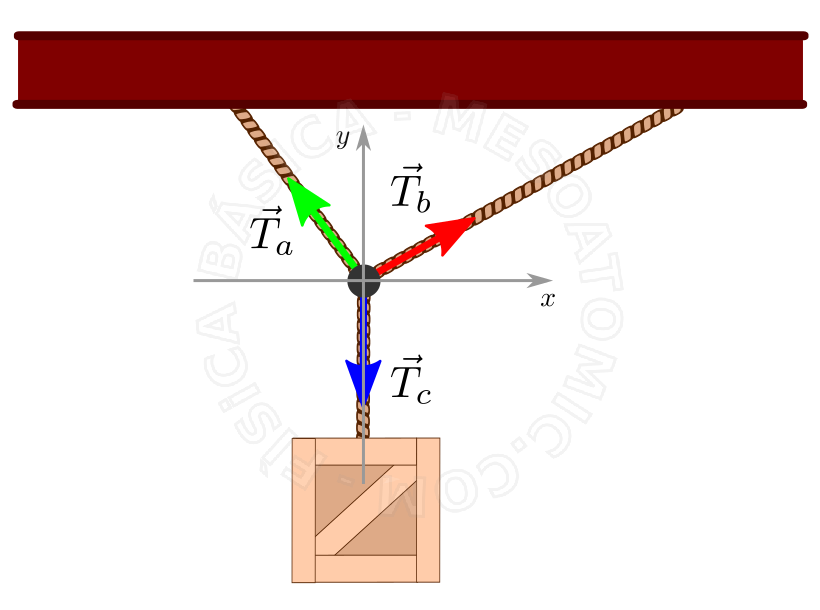
The above figure illustrates a problem which can be resolved by considering only a punctual particle, in this case, the node between the ropes. The net force is: $$ \vec{F}_{net} = \sum_i^n \vec{T}_i = 0,$$ or explicitly: \begin{array} \\ F_{net,x} &= -T_{a, x} + T_{b,x} + 0 = 0,\\ F_{net,y} &= +T_{a, y} + T_{b,y} - T_{c,y} = 0, \end{array} where the tractions (\(T_{i,j}\)) are positive numbers.
