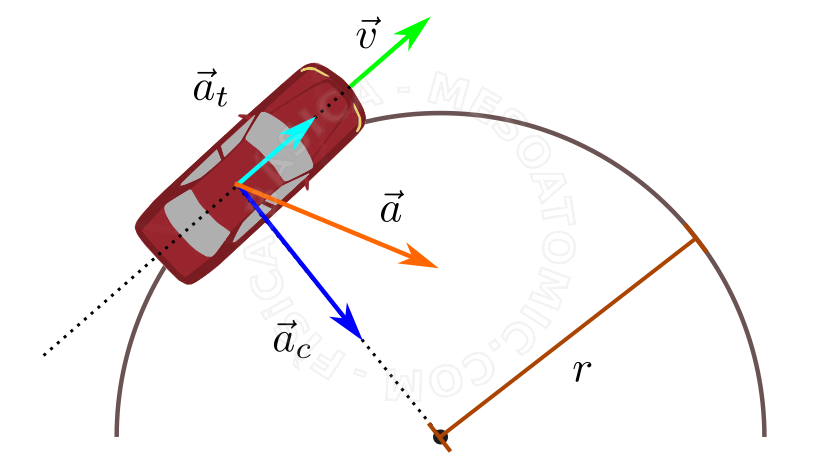
The figure above shows some vectors in a two-dimensional movement (circular path), which can be understood as follows:

Velocity vector \((\vec{v})\)

The velocity vector is always tangent to the trajectory at the point where the object is located and has the same direction as the motion.

Tangential acceleration vector \((\vec{a_t})\)

It is the acceleration component that dictates the variation of the speed module. It is in the same line of the speed, always. For an accelerated motion, \( \vec{a_t} \) has the same direction of the speed, and for a decelerating case, \( \vec{a_t} \) has an opposite direction to the speed.

Centripetal acceleration vector \((\vec{a_c})\)

It is the acceleration component that changes the velocity direction, and its direction is pointing towards the center of the path from the object position.

The acceleration module at a given instant is $$ a_c = \frac{v^2}{r} $$ where \(v\) is the speed module and \(r\) is the curvature radius of the path in the instant considered.

Resultant acceleration vector \((\vec{a})\)

It is the sum of all accelerations that act on a body. Vectorially, \( \vec{a} = \vec{a}_t +\vec{a}_c \); algebraically, \( a^2 = a_t^2 + a_c^2 \).