When we observe a phenomenon in nature, we can do this from different places and ways. For example, when watching the movement of a car, we can observe it by standing on a sidewalk or we can observe inside another moving car. Be that as it may, it is important that the analyses of the movement be consistent, regardless of whose referential we adopt.

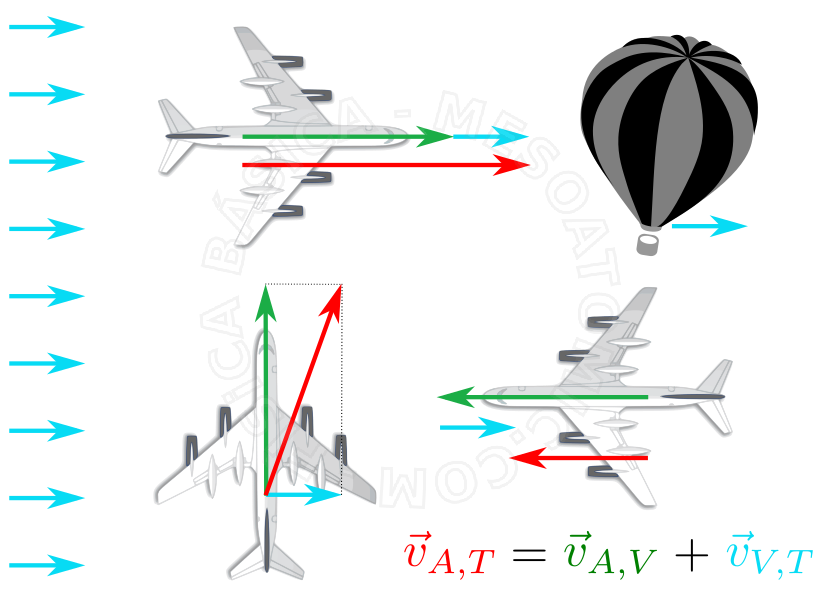
The correct way to observe a phenomenon is to adopt a referential and a coordinate system.  For example, suppose that the same phenomenon has been observed from two references, identified by  \(M\) and \(N\), where the system \(N\) moves in a straight line relative to the system \(M\), with relative speed \(v_{ M, N}\). With \( v_{A,N}\)being the speed of a car \(A\), known in the reference \(N\), we may want to know what is the corresponding velocity value \(v_ {A,M}\) of the car \(A\) on referential \(M\). The concept of relative movement allows us to answer this type of question.

Relative Motion

The equation for transforming from one reference to another is known as Galileo's transformation and has the following form: $$\vec{v}_{A,M} = \vec{v}_{A,N} + \vec{v}_{N,M},$$ where \(\vec{v}_{A,M}\) is the speed \(A\) in the reference \(M\), \(\vec{v}_{A,N}\) is the speed \(A\) in the reference \(N\) and \(\vec{v}_{N,M}\) is the speed of reference \(N\) in relation to \(M\).

Principle of movement independence (Galileo's principle)

When a body is under the simultaneous action of several movements, each of them is processed independently of the others. The figure below illustrates a typical case of relative motion.