- Mechanics
- /
- Kinematics
- /
- Basic motions
Consider a car that is pouring oil, so that oil drips at equal intervals of time. The positions of the oil marks on the track can be used to understand the movement of this car. In the following animation, see what happens if we plot the moment the drop of oil fell, \(t \), versus the position, \(s \). Test the limit cases: zero acceleration and an initial velocity other than zero; initial zero speed and non-zero acceleration. (The acceleration is constant throughout the movement)
Uniform Motion
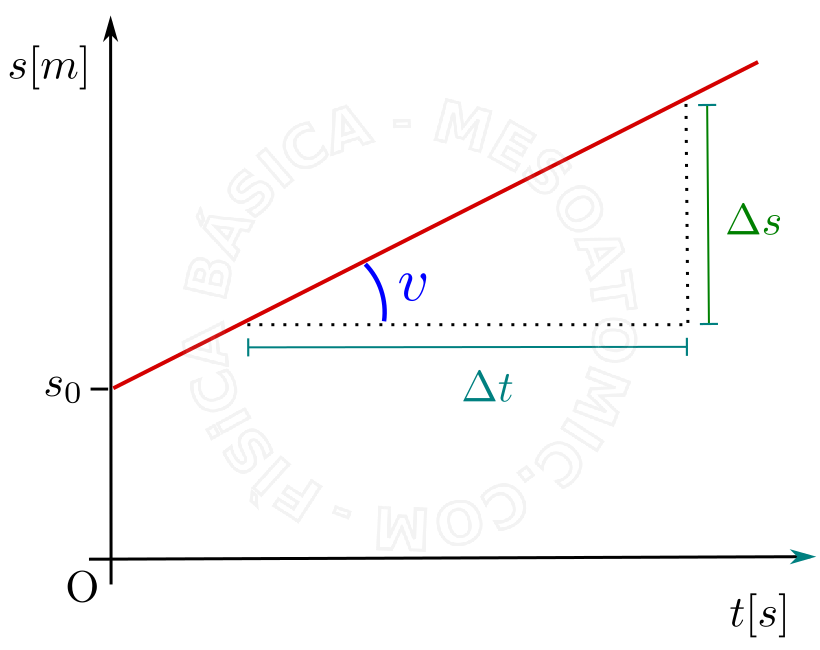
It is a movement in which the scalar speed is constant and different from zero \(v(t) = v_0 = \mbox{constant} \ne 0 \). The position as a fuction of time, for this movement, is: $$ s(t) = s_0 + v_0 t.$$
The figure below illustrates the graph \(s \times t\) of this movement, which, in this case, is always a straight line, that increases with time if \(v_0 \gt 0\) and decreases with time if \(v_0 \lt 0\).
Uniformly accelerated motion
Uniformly varying motion is the movement in which scalar acceleration is constant and nonzero, \(a(t)=\mbox{constant} \ne 0\).
The functions for this type of movement are:
- The position as a fuction of time
- $$ s(t) = s_0 + v_0 t + a \frac{t^2}{2}. $$
- The speed as a fuction of time
- $$ v(t) = v_0 + a t.$$
- The Torricelli's equation
- $$ v^2 = v_0^2 + 2 a \Delta s, $$ and, in this case, \(v\) is related to \(\Delta s\).
Graphics and interpretations
The graphics for this movement and their interpretations are presented below.
- Space \(\times\) time \((a > 0)\)
-

- Space \(\times\) time \((a < 0)\)
-

- Speed \(\times\) time \((a > 0)\)
-
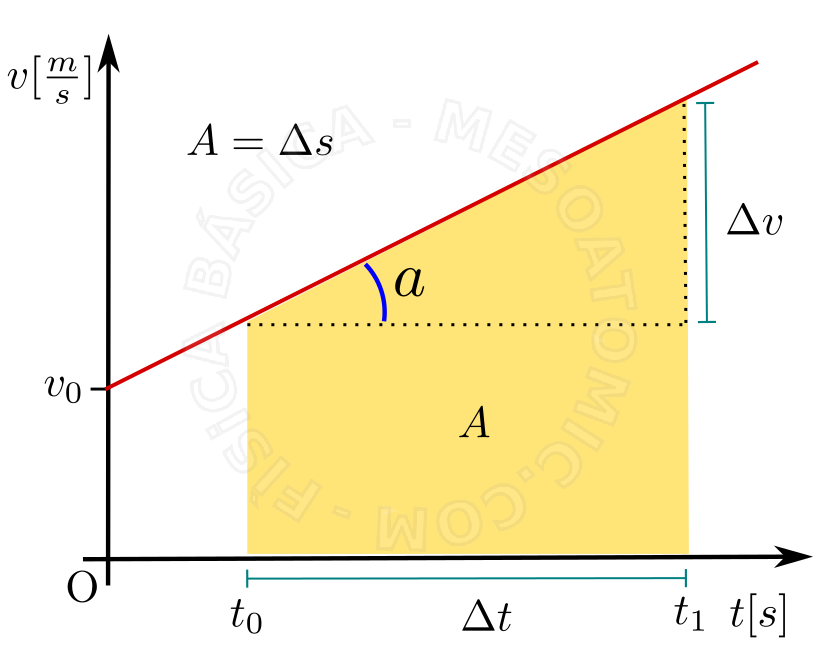
The area \(A\) under the graphic curve \(v \times t \), yellow region, is the distance traveled by the object from \(t_0\) to \(t_1\). In the same graph, the acceleration is given by the slope of the line, therefore, if the acceleration was negative, the graph would be a straight line inclined downwards.
