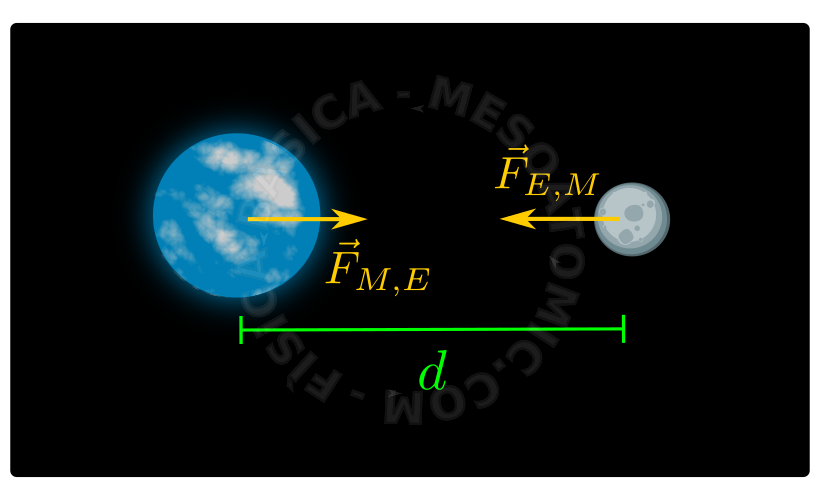
Considering the two bodies represented in the above figure: one with a mass \(M\) and another with mass \(m\) , separated by a distance \(d\) , a gravitational attraction will occur between them, whose intensity is: $$ F = G\frac{ M m }{d^2},$$ where \(G\) is a constant of modulus \(6.67 \times 10^{-11} N(\frac{m}{kg})^2\). The directions of forces are in a straight line connecting the centers of objects, and the direction is from one object to another, as shown in the figure.

Kepler's Laws

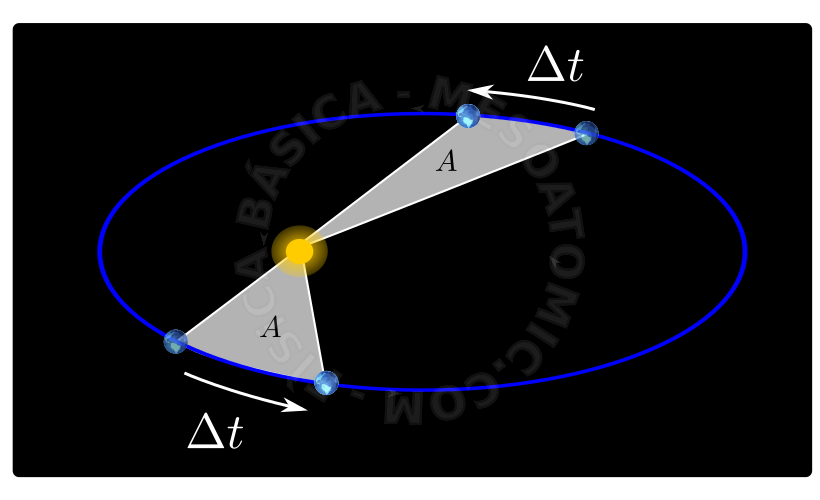
As a result of the attraction that the celestial bodies exert on each other, the following laws can be deduced. They were discovered by Kepler.

\(1^a\) - Orbits Law

The planets describe elliptical paths, where the Sun occupies one focus of the ellipse.

\(2^a\) - Areas of Law

The area swept by the radius vector of a planet fills out equal areas in equal times (see figure above).

\(3^a\) - Law of Periods

The cubes of the average radius of the planets around the sun are proportional to the squares of the periods of revolution. Or mathematically: $$ R^3 = k \tau^2,$$ where \(R\) is the average radius, \(\tau\) is the period of rotation around the sun and \(k\) is a constant.

Note: The farther a planet is from the Sun (larger radius), the greater its period of rotation around the Sun ( the greater the \(\tau\) ).