- Mechanics
- /
- Dynamics
- /
- Elastic forces
In nature, it is possible to find different types of materials with different properties. Here we will cover the elastic properties of the materials, which is the tendency to return to its initial state (equilibrium) when deformed. Examples of objects with such properties are: springs, rubber bands, fishing rod, and many others.
Elastic Forces
Elastic forces \(\vec{F}_e\) have the following characteristics:
- Direction
- When a body is deformed by a force, a tensile force in the opposite direction of the applied force is generated. The tensile force always has the directon to return the body to its initial state, equilibrium position.
- Module
- The magnitude of the elastic force depends on the type of material and the size of the deformation. For small deformations (within the elastic limit of the material in question) Hooke's Law can be applied, see below.
Hooke's Law
For an spring made of an elastic material, within the elastic limit, it is possible to consider that the intensity of the restoring force of the spring is proportional to the deformation made on it. Mathematically, this is: $$ F_e = - k \Delta x, $$ where \(k\) is the spring constant, which is different for different materials, and \(\Delta x = (x - x')\) is the deformation undergone by the spring with respect to the natural position of the spring, \(x`\) . The figure below illustrates this phenomenon.
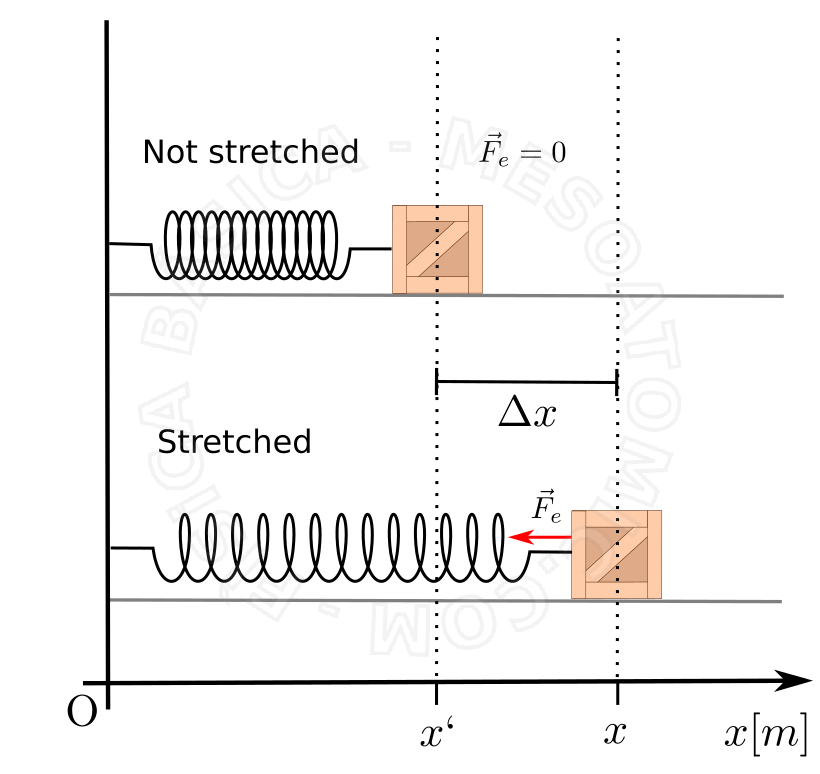
- The spring constant \(k\) is a measure of its "hardness"; that is, for a higher value \(k\) a greater force is needed to produce the same deformation.
- The force does not depend on the physical length \(L\) of the spring, but instead, depends on the deformation \((x` - x\) ) of the free end of the spring.
- Sometimes it is possible to consider a spring to be ideal, i.e., we can neglect the mass of a spring when compared to the mass of an object attached to it, and it will also always return to its initial state without permanent deformation.
