- Mechanics
- /
- Dynamics
- /
- Contact forces
The forces between surface, or contact forces, are essential for the analysis of mechanical systems. They are divided into two components: the normal forces and frictional forces.
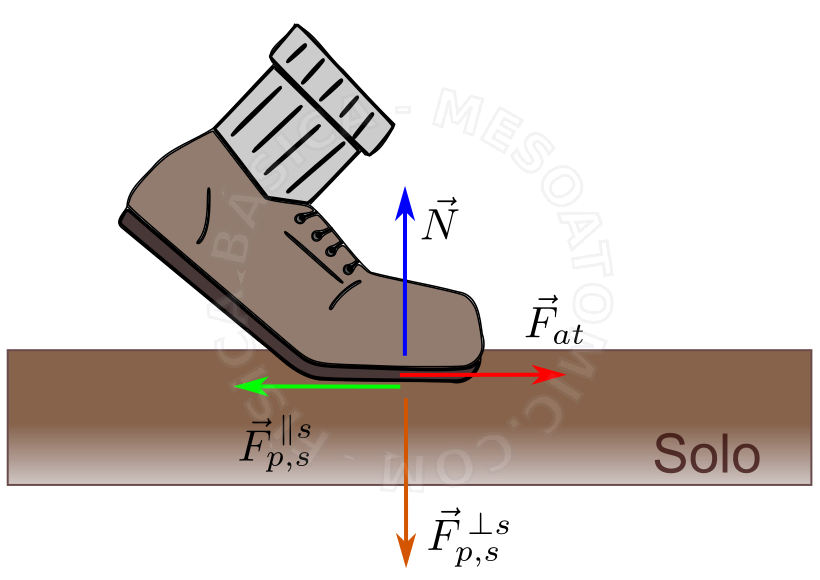
The figure above illustrates the superficial forces acting on the system foot and ground. The normal force \(\vec{N}\), which acts on the foot, is the orthogonal component of the reaction for the force that the foot does on the soil, \(\vec{N} = -\vec{F}_{f,g}^{\,\perp \, g} \) . And the frictional force, \(\vec{F}_{fric}\), is a force parallel to the surface, and is the reaction to the force that the foot does in the ground, \(\vec{F}_{fric} = -\vec{F}_{f,g}^{\,\parallel \, s}\) .
Normal Forces
A component of the force that appears in the contact between two surfaces is Normal, which is always perpendicular, or orthogonal, to the contact surface. This force can be understood using the law of action and reaction. When an object pushes the surface of another, this object will also be pushed with a force of the same intensity in the opposite direction.
Characteristics of Normal Forces
- Direction
- Always orthogonal or normal to the surface where the system of interest is in contact.
- Module
-
The algebraic value of the normal force can be found using Newton's second law. In the case of a system with mass \(m\), moving with acceleration \(a^{\, \perp \, s}\) perpendicular to the contact surface \(s\), the equation for the normal force is: $$N + \sum_i^n F_i^{\, \perp \, s} = m \, a^{\, \perp \, s},$$ where \( F_i^{\, \perp \, s}\) are the \(n\) algebraic values of the forces' modules perpendicular to the surface \(s\), besides the Normal, acting on the system. Important: in this equation is necessary to consider the module with the algebraic sign, indicating its direction, i.e., the algebraic value. The superscript \((\perp \, s )\) is to remind you that the calculation of the Normal force only uses the forces and accelerations perpendicular to the surface.
Frictional Forces
The frictional force is the force component parallel to the surface. It manifests itself between two contact surfaces when there is an external force, having a component parallel to the surface, is acting. This force is divided into two cases:
- Static Friction
- It is the force that acts when there is an external force trying to generate movement between surfaces, but there is no relative movement. The static friction force acts against this external force. The maximum static friction module that is possible between the surfaces is: $$F_{at(e)} \le \mu_e N,$$ where \(\mu_e\) is a constant that depends on the types of materials in contact, and \(N\) is the normal force in the system. Note that the force of static friction varies from zero to the maximum value. It will only have its maximum value if the sum of the components of the forces, that tend to move the object on a given surface, is equal to this maximum value.
- Dynamic Friction
- The dynamic frictional force, or kinetic friction, acts when an external force generates relative motion between two surfaces in contact. The module for the dynamic friction is always: $$F_{at(d)} = \mu_d N,$$ where \(\mu_d\) is a constant that depends on the types of materials in contact, and \(N\) is the Normal force to the contact surface.
Characteristics of Friction Forces
- Module
- Friction forces are proportional to the normal force \(N\) but there is a big difference from static to dynamic case.
- Direction
- It is always tangent to the contact surfaces where the system of interest is. And it is opposed to the relative movement between two surfaces, or the tendency to move.
- Irregularity of surfaces in contact
- Electromagnetic attraction between the two surfaces in contact.
