- Mechanics
- /
- Dynamics
- /
- Collisions
A collision is an isolated event where two or more bodies exert forces on each other, in a relatively short time interval.
Collisions
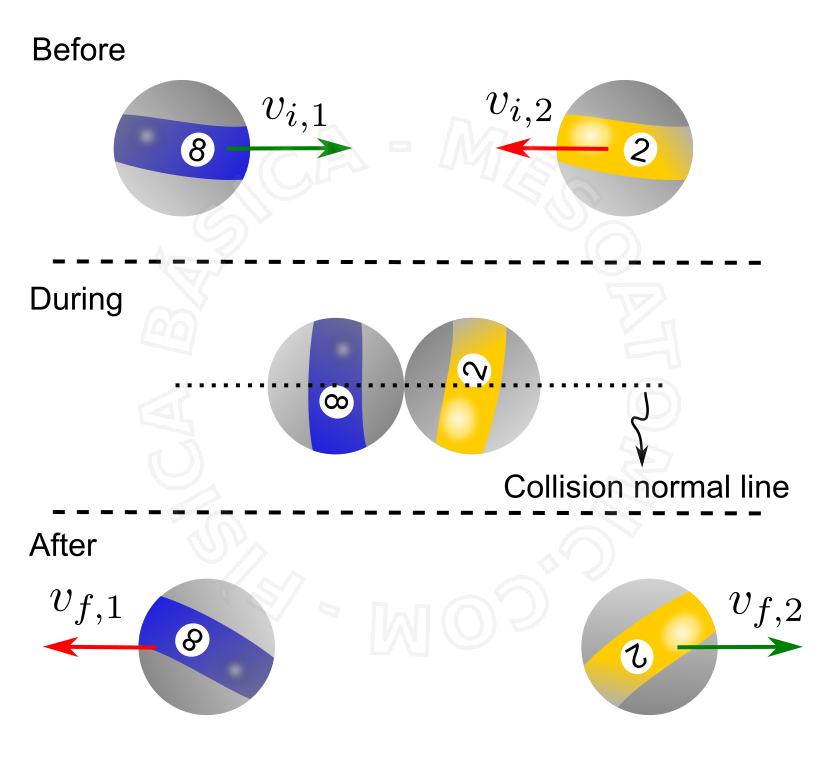
During a collision, the involved objects exchange very intense internal forces, called impulsive forces, in a relatively short time interval. These forces vary in a complex manner and cause deformations and changes in velocities of objects. Faced with high internal forces, we can generally neglect the external forces and consider the system, which is formed by objects colliding, as mechanically isolated. Thus, we can apply during a collision the Principle of Movement Conservation to mechanically isolated systems, that is: $$ P_i = P_f,$$ where \(P_i\) and \(P_f\) are, respectively, the initial linear moments, before the collision, and final moment, after a system crash. The following definitions are important:
- Collision Normal
- The normal line, perpendicular to the surfaces in contact during the impact is called collision normal.
- Central Collision
- If the centers of mass of the colliding bodies are located in the colision normal line, the shock is said to be central.
- Direct Hit
- If the speeds of the two material points are directed along the collision normal line, this is called a direct hit.
Energetic Aspect
When two objects collide, there is always a deformation stage. A second stage is also possible, the restitution stage, but it might not happen.
Coefficient of Restitution
For a given material, we can find experimentally what is the relationship between speed \(v_{after}\) at whitch the particles get away of each other after the collision, and the approach speed \(v_{before}\) before the collision. This relationship is named restitution coefficient \(e\): $$e = \frac{v_{before}}{v_{after}}$$ or $$e = - \frac{v_{i,2}-v_{i,1}}{v_{f,2}-v_{f,1}},$$ where \(v_{i,1}\) and \(v_{i,2}\) are the initial speeds of particles 1 and 2, respectively, and \(v_{f,1}\) and \(v_{f,2}\) are their final speeds.
It is important to note the following points:
- Speeds in the above equation should be used with its algebraic value, that is, with their respective signal.
- A billiard ball is slightly deformed when it collides, and quickly returns to its original shape. Therefore, the strength of interaction between two billiard balls can be considered quite conservative; that is, the collision is perfectly elastic.
| Central and Front Collision | Momentum | Kinetic energy | Coefficient of Restitution |
| Elastic | \(P_i = P_f\) | \(E_{k_i} = E_{k_f}\) | \(e = 1\) |
| Partially Elastic | \(P_i = P_f\) | \(E_{k_i} \gt E_{k_f}\) | \(0 \lt e \lt 1\) |
| Inelastic | \(P_i = P_f\) | \(E_{k_i} \gt E_{k_f}\) | \(e = 0\) |
