Current Element

Moving electrons form an electrical current. We call current element, the amount of electric charges that crosses orthogonally some portion of the conductor, at some time interval. The direction of this vector is the same of charges displacement. The electric current intensity unit in the \(IS\) is Ampere \((A = \frac{C}{s})\).

Magnetic Permeability \((\mu)\)

Different mediums will affect the magnet fields in a different manner, the magnetic permeability is used to account for this when calculating the force acting on a current element in the presence of a magnetic field in a specific medium. The permeability of vacuum (absence of material medium), represented by \(\mu_0\) , is: $$\mu_0 = 4 \pi 10^{-7} \frac{Tm}{A}$$ noting that \(\pi\)is worth approximately 3.14.

Lorentz Force

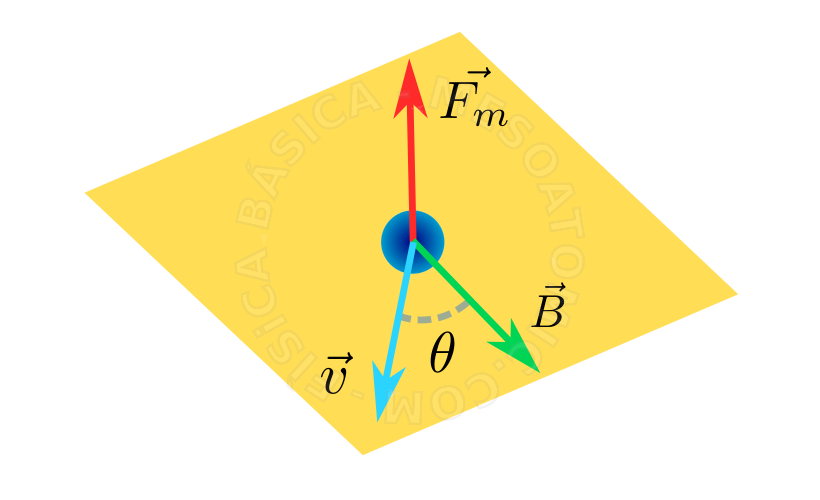
It is the magnetic force \(\vec{F_m}\) which acts on the electrified particle \(q\) when it moves with velocity \(\vec{v}\) in the region of a magnetic field \(B\). This force has the following characteristics:

Direction

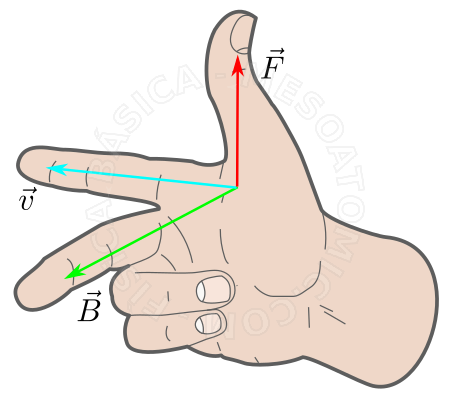
Perpendicular to the plane determined by \(\vec{v}\) and \(\vec{B}\), and it is given by the "right hand rule". When the charge \(q\) is negative, the direction is inverted.

Intensity

It is given by: $$F_m = qv B ~sen(\theta)$$ Where \(\theta\) is the angle between the vector \(\vec{v}\) and \(\vec{B}\) .

Applications of Magnetic Force

Loads in a Magnetic Field

A moving charge in a uniform magnetic field experiences a force that is perpendicular to speed. The trajectory of this charge is a circle and the centripetal force is the magnetic force itself. In the case of a charged particle of mass \(m\) and absolute charge \(|q|\), moving with velocity \(\vec{v}\) perpendicular to a uniform magnetic field \(B\), the radius of the circular path is: $$r = \frac{mv }{ q B}$$

Linear Conductor in a Magnetic Field

For a linear conductor of length \(L\), traversed by a current of intensity \(i\) immersed in a uniform magnetic field \(\vec{B}\) with \(\theta\) being the angle between the conductor and \(\vec{B}\), the magnetic force is given by: $$F_m = i BL ~ sen(\theta)$$

Force Between Conductors

Consider a long wire, traversed by an electric current. Consider an eletric current element that is parallel to the wire. It is found experimentally that the eletric current element is subject to the action of a force that has the following characteristics:

• There is an attractive force when the directions of the two currents, flowing through the wire and the current element, have the same direction. The force is repulsive if the direction of one current is in the opposite direction of the other;
• The strength of the force is directly proportional to the intensity of the current flowing through the wire, by the current element, and inversely proportional to the distance that separates them.

Rule of the Right Hand

Hall Effect